This post is part of a series on the parsing framework provided by Infragistics starting in version 12.2. The previous post in the series can be found here.
This time I want to talk about another real world ambiguity that can occur when writing grammar rules. This one is known as the dangling else ambiguity and can happen if a language has an if-then-else construct with an optional else. C# is a good example of such a language, so we’ll work with that.
Let’s define a simplified version of C# that has the ambiguity first:
Statement =
MethodInvocation
| Block
| IfStatement;
MethodInvocation =
IdentifierToken, '(', ')', ';';
Block =
'{', {Statement}, '}';
IfStatement =
'if', '(', Expression, ')', Statement, ['else', Statement];
The definitions for Expression and IdentifierToken have been omitted here, but their definitions are pretty straightforward: Expression is a non-terminal symbol representing a valid C# expression (preferably one that evaluates to a Boolean value), and IdentifierToken is a terminal symbol representing a valid C# identifier.
Notice that one type of statement in this grammar is a block. So anywhere a statement can be used, so can a group of statements surrounded with curly braces. This actually isn't necessary to demonstrate the ambiguity, but I included it to show how an if statement with braces and multiple statements could be allowed when if and else clauses only contain a single Statement within them.
Among others, this grammar allows for single-line if statements:
if (x)
A();
Multi-line if statements:
if (x)
{
A();
B();
}
If-else statements:
if (x)
A();
else
B();
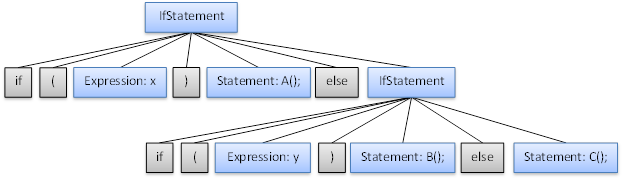
And If-else if-else statements
if (x)
A();
elseif (y)
B();
else
C();
The last example may not be so obvious, but here is how it is valid based on the grammar: from the 2nd‘if’ keyword to the end of the text is a single Statement belonging to the first ‘else’. The syntax tree for this code would look something like this: (the children of some Expression and Statement nodes have been excluded):
The ambiguity arises when the parser encounters something like the following text, which has had the indenting removed to highlight the ambiguous nature of it:
if (x)
if (y)
A();
else
B();
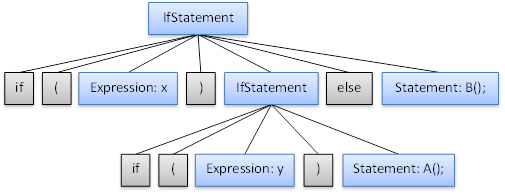
It is clear that the first if statement has a nested if statement under it, but what is unclear is whether the else clause is the alternative to the root if statement, as in
if (x)
if (y)
A();
else
B();
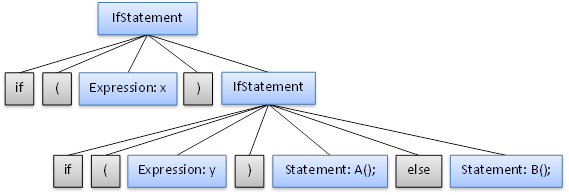
Or the alternative to the nested if statement, as in
if (x)
if (y)
A();
else
B();
We can also view the parse trees of these choices. The else associated with the root if statement looks like this:
And the else associated with the nested if statement looks like this:
So which one is correct? Well, in all programming languages, the latter is preferred (I believe this is true, but let me know if there is a language where the former is preferred). The general rule is that an else clause should be associated with the (lexically) closest if statement above it with which it can be associated. So the proper indentation of the text above is this:
if (x)
if (y)
A();
else
B();
This ambiguity is a problem and must be resolved somehow. One way to resolve this issue is to simply change the definition of the language itself. Making braces required under if statements or having some sort of “End If” marker like VB does will remove the ambiguity. But if you don’t want to do this or if it is not possible (maybe you are writing a grammar to parse an existing language which can’t be changed, like C#) there are a couple of ways to fix this without changing the language.
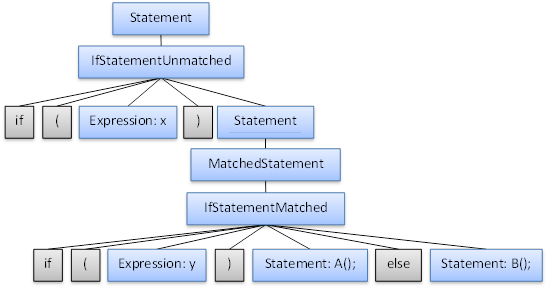
One way is to write the grammar rules in such a way so that no ambiguity occurs at all with the example we have here. To do that, we have to find a way to disallow the 1st ambiguous tree above. The problem with that tree is it allowed an if statement without an else clause to be the first statement of an if statement with an else clause. That else clause should have been matched with the nested if statement and not the outer if statement. To prevent this from happening, we have to split up the concept of statements into matched and unmatched statements. An unmatched statement will be an if statement without an else clause or an if statement which contains an unmatched statement (Note: in the case where an if statement does have an else clause and contains an unmatched statement, meaning it is also considered unmatched, the nested unmatched statement must appear in the else clause, because otherwise, it would allow for the erroneous tree from above again). A matched statement will be any non-if statement or any if statement which has an else clause and contains only matched statements. Here is what the grammar would look like:
Statement =
MatchedStatement
| IfStatementUnmatched;
MatchedStatement =
MethodInvocation
| Block
| IfStatementMatched;
MethodInvocation =
IdentifierToken, '(', ')', ';';
Block =
'{', {Statement}, '}';
IfStatementMatched =
'if', '(', Expression, ')', MatchedStatement, 'else', MatchedStatement;
IfStatementUnmatched =
'if', '(', Expression, ')', Statement
| 'if', '(', Expression, ')', MatchedStatement, 'else', IfStatementUnmatched;
Notice that each if statement with an else clause must have a MatchedStatement before the ‘else’ keyword. This prevents any nested if statement without an else clause from being just before an ‘else’ of an owning if statement and therefore disallows the incorrect tree from above. Here is what the syntax tree would look like using this grammar (some of the nodes here would normally be pruned from the tree but are left in to show which symbols would have been reduced):
While this grammar does remove the ambiguity, I see a couple of problems with it. First of all, if you want to write code to walk over the syntax tree and you have any logic specific to if statements, that logic now needs to be used for two node types: IfStatementMatched and IfStatementUnmatched. But the main problem I see with this grammar is that it is not intuitive. It takes some time to wrap your mind around the relationships between Statement, MatchedStatement, and the different kinds of if statements and there are complex and overlapping ownership roles for the various symbols here. This could cause issues with maintainability. If a new statement type is added in the future, it may be added as an alternative to the wrong statement symbol if someone doesn’t understand the relationships correctly.
So is there a better solution? It depends. If having these ambiguous structures appear in code files is not expected to happen often, which is probably a good expectation, then it might be acceptable to allow the ambiguity since it should not hurt performance negatively in the rare circumstances when it comes up. I am assuming this will be rare because an ambiguous if statement is not only ambiguous to the parser, but it is also ambiguous to the coder. So he or she will probably use braces to disambiguate these kinds of statements so the code is more readable. But if we allow the ambiguity, no matter how rare it may be, we still have to tell the parser that the latter ambiguous tree is preferred over the former, because otherwise it will arbitrarily pick one tree and that may be the wrong one.
And luckily, the NonTerminalSymbol.HasPriority property is great for disambiguating between two alternate parse trees for the same content. In this case, the tree we prefer has the if statement without an else clause higher in the tree than the if statement with the else clause. So if we separate the if statement into two helper non-terminal symbols representing if statements with and without else clauses and give priority to the one without, the tree with that symbol closer to the root (a.k.a. the correct tree) will always be chosen when an ambiguity occurs:
Statement =
MethodInvocation
| Block
| IfStatement;
MethodInvocation =
IdentifierToken, '(', ')', ';';
Block =
'{', {Statement}, '}';
IfStatement =
_ifStatementWithElse
| _ifStatementWithoutElse;
_ifStatementWithElse =
'if', '(', Expression, ')', Statement, 'else', Statement;
?<NonTerminalSymbolOptions HasPriority="true" />?
_ifStatementWithoutElse =
'if', '(', Expression, ')', Statement;
Even though _ifStatementWithoutElse will be pruned from the syntax tree when “based on name” tree pruning is used, its priority setting will still be honored and the tree which would have contained it higher in the node structure is preferred over the other. In addition to resolving the ambiguity, this grammar doesn’t have the problems of the previous grammar: logic which needs to work for all if statements can be written for the IfStatement nodes and this grammar is intuitive because all statements are contained directly under the Statement node and there are no complex relationships here.
Next time I’ll discuss the new APIs available in 13.1 for detecting and resolving ambiguities, both when writing a grammar and while parsing documents. After that, I will most likely move on to a new topic. But if you’d like me to discuss or revisit anything about ambiguities that is unclear or you think is worth mentioning, please let me know.
The examples used in this post and the unambiguous grammar presented as the first solution to the problem were adapted from “Compilers: Principles, Techniques, & Tools – 2nd Edition” section “4.3.2 – Eliminating Ambiguity”.
The information contained herein is provided for reference purposes only.
Copyright © 2013 Infragistics, Inc., All Rights Reserved.