I was about to write a post about ambiguities and I realized that before I do so, it is necessary for me to explain a bit more about how a (generalized) LR parser makes parsing decisions. And since I’m on the subject, I thought I’d explain a little bit why we chose to use an LR parser rather than an LL parser (another common parsing algorithm), because the way in which these parsers work factored heavily into our decision.
If you haven’t read my previous post introducing the Infragistics parsing framework here, I suggest you read it first.
As I mentioned in my previous post, the Infragistics parser is a type of LR parser, which is a bottom-up parser, meaning it starts the parse tree construction at the leaves and works its way to the root. LL parsers actually construct the parse tree in the opposite direction. Let’s take a closer look at how tree construction occurs with each parser type.
LL Parse Tree Construction
LL parsers, like LR parsers, read input from left-to-right (this is indicated by the first “L” in their names). When an LL parser starts parsing a document, it starts by creating the root node (the top of the tree). Then it decides which children to give that root node. So let’s say the start symbol for a grammar is called “S” and there are two productions with “S” as the head symbol (“A” and “B” are other non-terminal symbols):
- S → A
- S → B
Once the “S” node is created in the beginning of the parse, the LL parser must decide whether it should have a child node “A” or a child node “B”. How does it know? Well LL parsers are associated a number of look-ahead symbols. The general notation is LL(k), where k is the number of look-ahead symbols. So an LL(1) parser uses one symbol of look-ahead. This means that in the example above, the parser must decide whether to use “A” or “B” as a child by looking ahead at the next token from the lexer. If the parser were LL(2), the parser would be able to look at the next two tokens from the lexer. Typically, the k value is 1. If a grammar definition allows for unambiguous decisions about which production to use for any head symbol when looking at the next k tokens from the lexer, the grammar is said to be an LL(k) grammar. So if the productions for “A” and “B” in the above example are as follows (“c”, “d”, and “e” are terminal symbols):
- A → c d
- B → c e
Then the grammar is not LL(1), because when the “S” node is created and the next token from the lexer is <c>, the parser will not know whether to create an “A” or a “B” as the child node. However, this grammar would be an LL(2) grammar, because two symbols from the lexer would allow the parser to make the correct decision.
Once the LL parser decides which children to give the root node, it processes each child it just created, from left-to-right, as follows:
- If it is a terminal symbol, the parser checks to see whether it matches the symbol of the current token from the lexer. If so, the token has been matched and the lexer moves to the next token. If not, there is an error and the input is not correct.
- If it is a non-terminal symbol, the parser decides which children to give it by selecting the production to use, as described above. Then the parser processes each of the new children recursively before processing the next child from the current level (the parser does a depth-first traversal of the tree as it creates it).
So the following might be a parse tree structure generated by an LL parser. The labels indicate the order in which the nodes were processed:
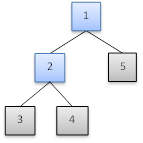
One downside to LL(k) parsers is that they cannot handle left-recursion (when a production has the head symbol as the first symbol of the body) without going into an infinite loop. For example, let’s say the start symbol instead had these two productions:
- S → S A
- S → B
If the first token from the lexer indicates that production 1 should be used, the root “S” node will be given children “S” and “A”. Then the first “S” child node will be processed. It will look at the first token from the lexer (which hasn’t changed) and determine that this “S” node should also be given children “S” and “A”. It will then look at the same token from the lexer and give that “S” the same children again, and so on. Left-recursion can be removed from a grammar in most cases, but although the same language can still be parsed by the corrected grammar definition, the grammatical structure of the tree could be changed dramatically, which could require a lot of additional work on the part of the developer when analyzing the parse tree. Also, it could add a lot of over-head to logically treat the tree as if it had the original grammatical structure. This is one of the reasons we chose to not use an LL parser.
LR Parse Tree Construction
As I’ve already mentioned, LR parsers construct the parse tree from the bottom-up, which is the exact opposite of how LL parsers construct the tree. An LR parser will read tokens from the lexer from left-to-right as well, but it will start by making the first lexer tokens leaf nodes in a tree which doesn’t exist yet. They are just kind of floating in space for now. As soon as the parser has moved past the body of a production, it will perform a reduction which creates the parent node representing the head symbol of that production. The nodes representing the production body, which were previously floating in space, are now children of the new parent node. They are not floating, but their parent node is. It will stay that way until it is in the body of some other production which is reduced, and then it will get a parent as well. This process continues until the last parent node created is the node representing the start symbol of the grammar, which becomes the root node of the final parse tree. So let’s look at an example of this. Let’s say we have a grammar defined with the following productions and “S” is the start symbol of the grammar (uppercase letters are non-terminals and lowercase letters are terminals):
- S → a X c
- X → b
And let’s say the lexer has the tokens <a><b><c>. The parser reads the first token and creates a leaf node to represent it:

This does not form a full production body, so the parser reads the next token, <b>, and creates another leaf node:

The parser has now moved past the full production body for the production X → b, so it performs a reduction and creates a parent node to represent “X”, the head of the production:
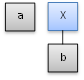
“a X” is not a full production body, so the parser moves to the next token, <c>, and creates another leaf node to represent it:
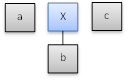
The floating nodes, “a X c” do form a full production body for the production S → a X c, so it performs another reduction and creates a parent node to represent “S”:
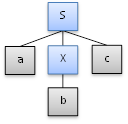
And since “S” is the start symbol and there are no more tokens from the lexer, the parse is complete.
That was a rather simple example but let’s say there were a few more productions in the grammar:
- S → a X c
- S → a Y d
- X → b
- Y → b
Now when the parser moves past the <b> and gets to this configuration:

it doesn’t know which production to use to reduce the “b” node. Both X → b and Y → b are valid in this context. So to solve this problem, the LR parser also uses look-ahead symbols. And similar to LL(k), LR parsers are generally written as LR(k) where k is the number of look-ahead symbols. So an LR(1) parser uses one symbol of look-ahead. In this case, an LR(1) parser would read the next token from the lexer, which is <c>, and see that the Y → b reduction is not correct because “Y” cannot be followed by a “c” terminal symbol. Grammars which can unambiguously allow an LR(k) parser to choose the correct production after reading the next k input symbols from the lexer are known as LR(k) grammars.
Although this concept of look-ahead seems similar between LL and LR parsers, they are actually used in entirely different ways. The LL(k) parser uses the next k symbols from the lexer to determine which production it will start creating whereas the LR(k) parser uses the full production body plus the next k symbols from the lexer to determine which production it has finished creating. LR(k) parsers defer the production decision until the end of reading the full production. Here is another way to look at it:

For this reason, there are far more LR(k) grammars than LL(k) because they allow the parser more symbols in which to determine what to do. Every LL(k) grammar is an LR(k) grammar, but not every LR(k) grammar is an LL(k) grammar (for the same k values). This is a major reason why we chose to create a type of LR parser: it can accommodate a wider variety of grammar definitions without needing to handle ambiguities. Our parser does handle ambiguities, but it is faster if it doesn’t have to.
Now, I want to point out that there is nothing wrong with LL parsers. I actually implemented a recursive-descent parser, which is a type of LL parser, to parse Excel formulas in our Excel library. Recursive-descent parsers are much easier to create by hand and allow for the developer to easily add custom logic at each step of the parsing process. That is fine for creating a parser by hand to parse documents in a specific language. LR parsers, on the other hand, usually require a code generation process because the decision making logic the parser requires is much too difficult to create by hand. But the parsing framework we created was not designed to parse documents in one specific language. It was designed to parse documents in an arbitrary grammar provided by you. We wanted to be able to handle as many of your grammars as possible, so an LR parser was the best choice for us.
Before I go, I just remembered something about LR parsers which will be very important when I discuss ambiguities. Because LR parsers defer the creation of parent nodes until they have read through a full production body, they do a very good job at “constructing” multiple production bodies at once. It can know that it is potentially in the middle of 10 different production bodies without knowing which one it will eventually create and no ambiguities will occur. But what does cause an ambiguity is when one or both of the following occurs:
- The next k tokens from the lexer tell the parser that two or more different productions are complete and can be reduced to their head symbols.
- The next k tokens from the lexer tell the parser that a production is complete and can be reduced to its head symbol, but the first of those tokens also moves the parser along in a different production body which is not yet complete.
I will go into more detail on what to do about this next time.
The information contained herein is provided for reference purposes only.
Copyright © 2012 Infragistics, Inc., All Rights Reserved.